Función Coseno

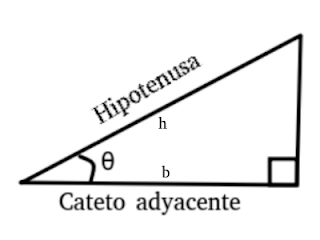
La función trigonométrica coseno nos relaciona al lado adyacente a un ángulo con la hipotenusa del triángulo, en un triángulo rectángulo.

Así tenemos que:

Ahora observemos el comportamiento del coseno a través de un estudio en el círculo trigonométrico.

 

En el círculo trigonométrico la coordenada del  cateto adyacente viene dada por la coordenada x del punto P (x,y), veamos las características del coseno en el círculo trigonométrico.

1.-Veamos que cuando el punto p(x,y) se encuentra en (1,0) el cateto adyacente vale 1 de igual manera la hipotenusa vale 1, dado que la hipotenusa es constantemente igual al radio del círculo,  entonces el coseno del ángulo vale 1.

2.- Mientras el punto p(x,y) se encuentre en el primer cuadrante el lado adyacente al ángulo será positivo, por lo tanto el seno también.

3.- Cuando el punto p(x,y), se encuentra en el punto p(0,1), el cateto adyacente vale 0,así que el coseno del ángulo vale 0.

4.- Cuando el punto p(x,y) se encuentra en el segundo cuadrante el cateto adyacente es negativo así que el coseno es negativo.

5.-En el caso del punto p(-1,0)  como pasa en el punto p(1,0) el coseno toma como valor el 1, pero en este caso negativo dado que la coordenada x del punto p es igual a -1.

6.-Mientras el coseno se encuentra en el tercer cuadrante toma valores negativos, podemos notar entonces que los valores del seno y del coseno tienen el mismo signo en los cuadrantes I y III.

7.- Cuando el punto se encuentra en la coordenada (0,-1) el coseno toma como valor -1. 

8.- En el cuarto cuadrante a diferencia del seno el coseno toma valores positivos.

Con todo esto en mente trazamos la gráfica del coseno.

NOTA: Lo primero que se observa es que la gráfica del coseno es la misma que la del seno trasladada π/2 hacia la izquierda.

Ahora realizamos un análisis de la función:

Dominio: (-∞,∞)

Rango: [-1,1]

Crece en el intervalo (-π+2kπ,0+2kπ), k ∈ R

Decrece en el intervalo (0+2kπ,π+2kπ), k ∈ R

Es positivo en el intervalo  (-π/2+2kπ,π/2+2kπ), k ∈ R

Es negativo en el intervalo (π/2+2kπ,3π/2+2kπ), k ∈ R

Es concava hacia abajo en el intervalo (-π/2+2kπ,π/2+2kπ), k ∈ R

Es concava hacia arriba en el intervalo (π/2+2kπ,3π/2+2kπ), k ∈ R
Tiene mínimo en el punto (-π,-1) se repite con una frecuencia de 2π.
Tiene máximo en el punto (0,1) se repite con una frecuencia de 2π.

No posee límite cuando tiende al infinito o al menos infinito.

Es una función acotada por y=1 y y = -1 

Y no posee límite cuando tiende a infinito.

Corta al eje y en el punto (0,1)

Corta al eje x en el punto (π/2,0) con frecuencia π.

La rama principal del coseno se considera el intervalo [0,π].(La rama principal se considera por ser un intervalo en el cual la función es biyectiva y por lo tanto es ese intervalo la función coseno puede tener inversa)

La función inversa del coseno es el arcocoseno y la función recíproca es la cosecante.

Contenido relacionado

Función Seno 

Volver al contenido